다익스트라와 크루스칼 알고리즘에 관한 고찰

다익스트라 문제를 풀다가 크루스칼과 혼동이 와서 둘의 차이가 무엇인지 고찰해 봤다.

둘다 한 노드에서 출발하여 Priority Queue를 사용해서 다음 간선을 찾는 방식이라 혼동이 올 수있는데

그림에서 보듯이 두 알고리즘이 요구하는 그래프도 다르고 리턴하는 타입도 다르기 때문에 차이가 있다.

다만 그래프를 실제로 만들 필요는 없고 개념적으로만 존재한다고 생각하고 풀어야한다.

 

극단적인 그림을 그려 볼까?

이것처럼 다익스트라는 크루스칼이라면 절대 쓰지 않을 간선을 사용하기도 한다.

왜냐하면 다익스트라는 X에서 얼마나 가깝냐가 PriorityQueue의 정렬기준이고

               크루스칼은 직전 단계에 만들어진 그래프의 노드들에 연결된 간선중 가장 가중치가 작은 간선을 선택하기 때문

 

그럼 다익스트라가 생각하는 PriorityQueue와 크루스칼이 생각하는 PriorityQueue에 대해 고찰해보자

 

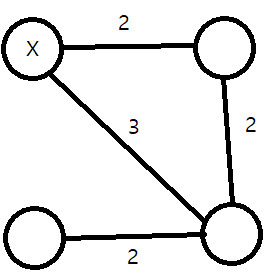
이런 데이터가 있다고 생각해보자 크루스칼은 다음과 같이 생각한다.

PriorityQueue는 간선의 가중치를 기준으로 삼는다.

그럼 다익스트라는 어떨까

먼저 x로 이어지는 가상의 간선(가중치 0)을 큐에 넣고 바로 poll 하자

도착지 노드에서 이어지는 간선을 큐에 넣자

새로운 간선은 X에서 부터 이어지는 가중치 합계가 들어가야 논리상 맞다.

큐에 가중치가 3, 4인 간선이 있었는데 3을 선택해서 도착지 B에서 연결된 간선들은 큐에 넣는다.

이제 큐에 가중치 4, 5인 간선이 있었는데 이 중 4를 선택한다. 그런데 도착지B에서 이미 있던 값 3과 새로운 가중치4를 비교한다. 4가 3보다 크므로 4는 버려 진다.

마지막남은 간선을 큐에서 poll 하고 새로 offer되는 간선이 없어서 반복문은 종료된다.

 

코드로 보자 N은 노드의 수다.

static int [] costing(HashMap<Integer, ArrayList<Vertex>> map) {
        int [] cost = new int [N+1];
    for (int i = 1; i <= N; i++) {
        cost[i] = Integer.MAX_VALUE;
    }
    cost[X] = 0;

   PriorityQueue<Vertex> pq = new PriorityQueue<>((o1, o2) -> {
       return o1.weight - o2.weight;
   });

   pq.add(new Vertex(X, 0));

   while(!pq.isEmpty()) {
       Vertex v = pq.poll();
       for (Vertex vertex : map.get(v.node)) {
           if (cost[vertex.node] > cost[v.node] + vertex.weight) {
               cost[vertex.node] = cost[v.node] + vertex.weight;
               pq.offer(new Vertex(vertex.node, cost[vertex.node]));
           }
       }
   }

   return cost;
}

여기까지가 전체코드다

for (Vertex vertex : map.get(v.node)) {
   if (cost[vertex.node] > cost[v.node] + vertex.weight) {
       cost[vertex.node] = cost[v.node] + vertex.weight;
       pq.offer(new Vertex(vertex.node, cost[vertex.node]));
   }
}

이 부분에서 볼 수 있듯 도착지에 미리 있던 코스트가 새로 추가될 코스트 보다 크면 새 간선을 추가해 주는걸 확인 할 수 있다.

 

그리고 크루스칼과 달리 방문여부를 판단하는게 아니라, 새로 추가되는 간선으로 인해 비용이 줄어드는지를 판단한다.